This (in-progress) post aims to stay up-to-date with the popular Transformer-based models.

Table of contents

Transformer

The Transformer (Vaswani et al., 2017) is undoubtedly one of the most impactful works in recent years. It took the NLP world by surprise by achieving state-of-the-art results in almost every language task, and it is now doing the same for audio and vision. The model secret recipe is carried in its architecture and so-called “self-attention” mechanism.

Self-attention

Attention (Bahdanau et al., 2014) is a mechanism to be learned by a neural network that relates elements in a source sequence to a target sequence by selectively concentrating on a relevant set of the information at hand. The amount of attention put on each element is given by the learned weights and the final output is usually a weighted average.

Self-attention is a type of attention mechanism that relates different elements of a single sequence (source and target are the same).

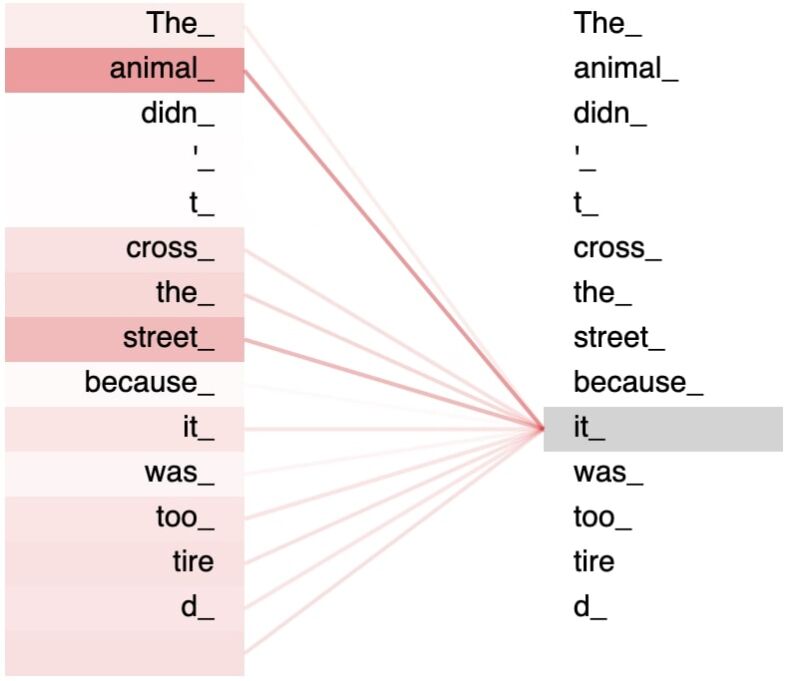
Fig. 1: Illustration of the self-attention mechanism. This example shows the attention brought to the word "it" from all the words in the sentence.
(Image source: Tensor2Tensor Google Colab)

The Transformer model relies on the scaled dot-product attention. Given a set of query, key, and value vectors (one of each for every term in the input sequence), the output vector of a given term is a weighted sum of all the value vectors in the sequence, where the weight assigned to each value is determined by the dot-product of the query vector with the corresponding key vector.

For each term \(t_i\) of an input sequence \(\{t_1, \cdots, t_n\}\), the self-attention mechanism performs the following steps:

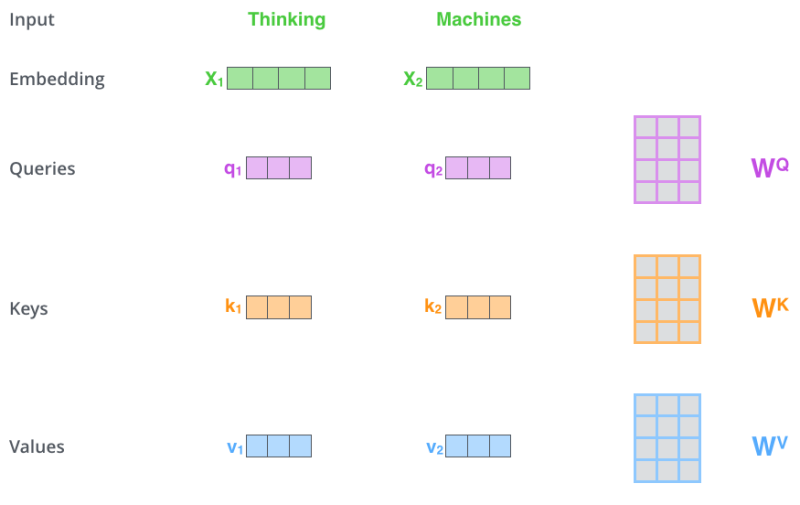
  1. Query, key, value. Compute the query, key, and value vectors by multiplying the initial term embedding \(\boldsymbol{x}_i \in \mathbb{R}^{d_{\text{model}}}\) with the query weight matrix \(\boldsymbol{W}^{Q} \in \mathbb{R}^{d_{\text{model}} \times d_{k}}\), the key weight matrix \(\boldsymbol{W}^{K} \in \mathbb{R}^{d_{\text{model}} \times d_{k}}\), and the value weight matrix \(\boldsymbol{W}^{V} \in \mathbb{R}^{d_{\text{model}} \times d_{v}}\), respectively: \(\begin{equation} \begin{aligned} \boldsymbol{q}_i &= \boldsymbol{x}_i \boldsymbol{W}^Q, \\ \boldsymbol{k}_i &= \boldsymbol{x}_i \boldsymbol{W}^K, \\ \boldsymbol{v}_i &= \boldsymbol{x}_i \boldsymbol{W}^V, \end{aligned} \end{equation}\)

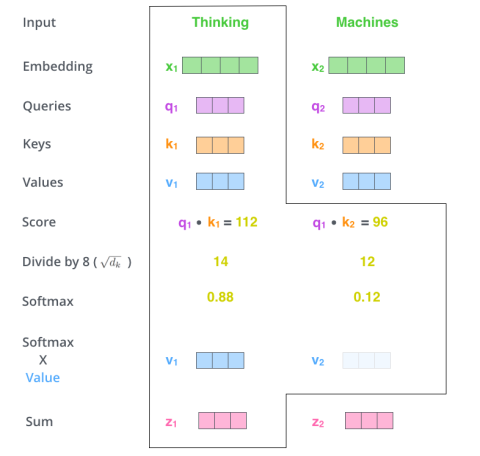
  2. Alignment scores. Score term \(t_i\) against all the other terms in the sequence by taking the dot-product of its query vector with all the key vectors of the sequence: \(\begin{equation} s_{ij} = \frac{\boldsymbol{q}_i \boldsymbol{k}_j}{\sqrt{d_k}}, \hspace{1cm} \forall j=1,...,n. \end{equation}\) NB: Dividing the scores by the square root of the key vector dimension aims at providing the dot-products to grow large in magnitude when \(d_k\) is large, which has the effect to push the softmax result into regions where it has extremely small gradients.

  3. Weights. Normalize the alignment scores by applying a softmax operation: \(\begin{equation} \alpha_{ij} = \frac{e^{s_{ij}}}{\sum_{j=1}^{n} e^{s_{ij}}}, \hspace{1cm} \forall j=1,...,n. \end{equation}\)

  4. Context vector. Sum up the weighted value vectors as the final context vector: \(\begin{equation} \boldsymbol{z}_i = \sum_{j=1}^{n} \alpha_{ij} \boldsymbol{v}_{j}. \end{equation}\)

Fig. 2: Illustration of the self-attention mechanism computed in vector form.
(Images source: Figures 10 and 13 in Jay Alammar, 2018)

In practice, the self-attention mechanism is computed on a set of queries simultaneously, packed together into a matrix \(\boldsymbol{Q} \in \mathbb{R}^{n \times d_k}\). The keys and values are also packed together into respective matrices \(\boldsymbol{K} \in \mathbb{R}^{n \times d_k}\) and \(\boldsymbol{V} \in \mathbb{R}^{n \times d_v}\). The output matrix is then computed as follows: \(\begin{equation} \text{Attention}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = \text{softmax}\left(\frac{\boldsymbol{Q}\boldsymbol{K}^\top}{\sqrt{d_k}}\right)\boldsymbol{V}. \end{equation}\)

Multi-Head Self-Attention

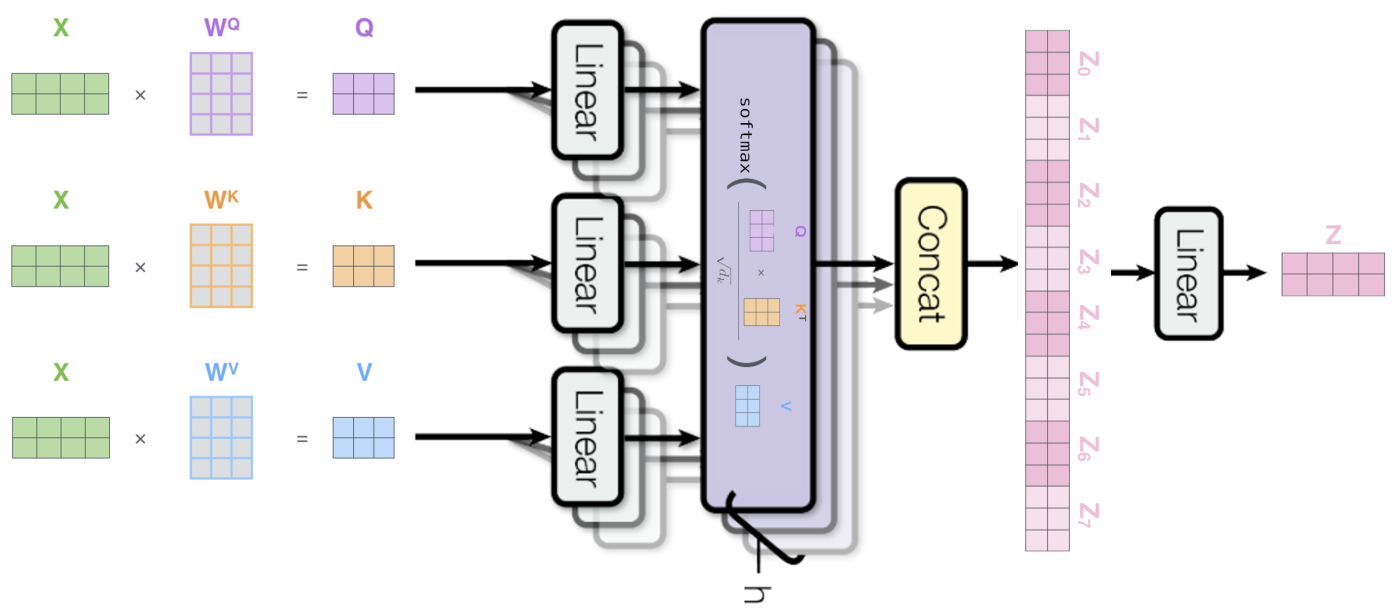
Rather than computing the self-attention once, the Transformer uses the so-called “multi-head” attention mechanism, where self-attention is performed in parallel on \(h\) different linear projections of the query, key and value matrices. This yields \(h\) different output matrices \(\boldsymbol{Z}_i \in \mathbb{R}^{n \times d_{\mathrm{model}}}\) called “attention heads”, which are then concatenated and projected into a final representation subspace: \(\begin{equation} \begin{aligned} \operatorname{MultiHead}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}) &=\text{Concat}\left(\boldsymbol{Z}_{1}, \ldots, \boldsymbol{Z}_{\mathrm{h}}\right) \boldsymbol{W}^{O} \\ \text{with } \boldsymbol{Z}_{\mathrm{i}} &=\text{Attention}\left(\boldsymbol{Q} \boldsymbol{P}_{i}^{Q}, \boldsymbol{K} \boldsymbol{P}_{i}^{K}, \boldsymbol{V} \boldsymbol{P}_{i}^{V}\right), \end{aligned} \end{equation}\) where \(\boldsymbol{P}_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}\), \(\boldsymbol{P}_{i}^{K} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}\), \(\boldsymbol{P}_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}}\), and \(\boldsymbol{W}^{O} \in \mathbb{R}^{hd_{v} \times d_{\text{model}}}\) are parameter matrices to be learned. According to the paper, “multi-head attention allows to jointly attend to information from different representation subspaces at different positions”.

Fig. 3: Illustration of the multi-head self-attention mechanism.
(Images source: Figures 14 and 15 in Jay Alammar, 2018, and Figure 2 in Vaswani et al., 2017)

Encoder-Decoder Architecture

[…]